The charter school movement is enjoying something of a renaissance in the United States. Charter schools—which receive public funding but are privately run, thus removing some features of normal public schools, notably established teachers’ unions—are one of President Obama’s priorities.  They are also the cause du jour for New York City’s hedge fund managers. Education policy wonks are understandably interested in whether charter schools really help students failed by the public system.

I am sceptical about the benefits of private sector involvement in public schools, but I’ve still been watching the debates with some interest. There has not been much research on Canada’s only charters, in Alberta, so most of what I read is from the States. That’s why I came across this post on Eduwonk.

In it, Andrew Rotherham observes that charters are over-represented in the U.S. News top 100 high school rankings. Since Rotherham introduced the post with “here’s one way to think about charter performance” I thought he meant this as evidence that charters are better schools in general. He has since responded to my comment, and clarified that he meant to make a narrower point. But I’d still like to explain my original objection, because there is a bigger lesson here.

Let’s imagine that we looked at a ranking of the best 100 schools in the US, and found that all 100 were charter schools. We might conclude that charter schools, on average, are better schools. But it could also be that charter schools are more variable—more likely to be very good, but also more likely to be very bad. Maybe the bottom 100 schools are all charters as well. Since we don’t have the full data set, we can’t tell.

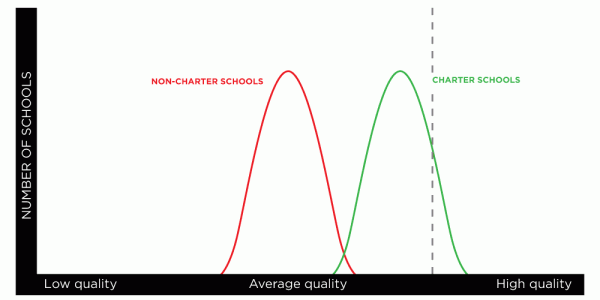
What we’re talking about is the difference between mean and variance. Mean is a fancy word for what you know as the average—an estimate of the centre of some data. Variance is a measure of how spread out that data is. It helps to look at the graphs below.

These curves represent an imaginary data set. The height of the curves shows how many schools are at each level of quality, which moves from low to high along the bottom. On these symmetrical curves, the mean is the same as the mode, or the quality level where the curve maxes out. The variance expresses how wide the curves are.

Now let’s imagine that we’ve taken a sample of the highest quality schools – say, everything to the right of the vertical dotted line. We’ve found that every school in our sample is a charter. In this graph, that’s because the distribution for charter schools is further to the right – they are, on average, better schools:

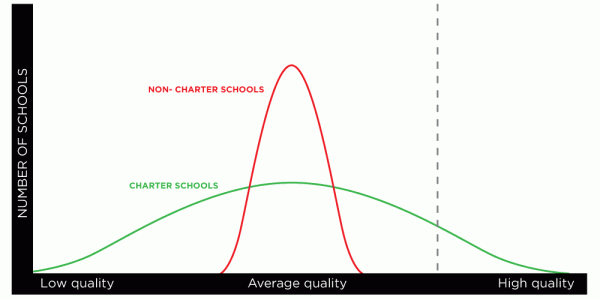
But in this second graph, we find a similar sample—all charter schools—even though the mean for both types of schools is the same. All our data reflects is that charter schools are more variable. A lot of them are very good, but a good number are very bad as well:

The way an introductory statistics textbook would put this is that you can’t select your sample based on the dependent variable. If you want to know what sort of diet will help you live longer, you can’t just interview your oldest relatives. If you want to know what sort of training will make you run faster, you can’t just talk to Olympic gold medalists. You won’t have the full picture, and everything that is special about these high achievers could be true of other, less successful eaters or runners. Informally, and in the press, we make this mistake all the time.

I said that this data set was imaginary for a reason – you shouldn’t draw any conclusions from my hypotheticals. A lot of different factors make measuring charter school performance difficult, so research is mixed. But there are reasons to believe that the U.S. News data might at least in part be reflecting higher variance. If charter schools have to follow fewer rules, it makes sense that they would vary more than normal public schools.

This isn’t something that charter advocates dispute. As two Eduwonk guest bloggers put it in October: “Say you set out to improve your mother’s beloved spaghetti sauce recipe. […] You try ten different variations.  Despite your best efforts, three are worse than the original.  Five are no better, but two are markedly superior.  On average, the new batches are a little worse than your mom’s. But—would you say your experiment was a failure, or a success? It really depends on what you do next.” Proponents of charter schools want to shut down bad schools, and learn from good schools. As Rotherham wrote in his response, “in practice there are elements of state policy that can move the quality curve substantially to the right.”

This might be why education reformers are so focused on a relatively small number of successful models, like the Knowledge is Power Program and Green Dot Public Schools. These reformers are fine with high variance, and interested in the upper tail of the distribution. But over the long run, they will also need to prove that they can move the whole curve to the right.